We need to determine the mathematical relationship between
degrees C and degrees F. Here is an animation
determining this relationship. This data was obtained by
simultaneously measuring the temperature of a sample of ethanol
in both degrees C and degrees F. This data is plotted with
degrees F on the y-axis and degrees C on the x-axis.
To begin the problem we must determine the range of the scale on
both axis. On the y-axis the data ranges from -103 to
+172, so we'll set a range of -125 to +175 in 25 degrees
increments. On the x-axis the scale will range from -100
to +100 degrees C. By using these scales we'll be able to plot
all of the data points.
So now plot the data. In the animation each pair of data
points is identified as the data is plot on the graph. Next draw
the best straight line through the data. The general equation for
a straight line is given as y = mx + b where m is the slope of
the line and b is the intercept on the y-axis at x
= 0.
First determine the slope of the line. Select two points
which fall exactly on the line. Usually these two points are not
data points. The slope is determined by measuring the change in y
(rise) and dividing by the change in x (run). So selecting
the two data points and determine the rise, and then the run. The
ratio is 100 divided by 55, which nearly 99 divided by 55, which
is 9/5's.
The y- intercept can be determined by moving the y-axis
over to the point where the line intersects with x=0. We
see this is at 32.
So putting the results together we can determine the equation
for the line.
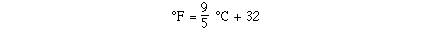
![]()