In Chapter 2 we explored some of the experimental
evidence which has lead to our modern view of the electronic structure of the
atom. The atom contains protons, neutrons and electrons
Rutherford is credited with our current view of the atom..a
nucleus containing the majority of the mass of an atom made up of
protons and neutrons with the electrons outside the nucleus. Our
goal in this chapter is gain a better understanding of the model
of the electron's behavior.

Classically the electron was viewed as `orbiting' the
nucleus. The concept of an orbit, like the moon travelling around
the earth, suggests a defined path which allows the exact
determination of the position of the moon. It allows up to
predict exactly were the moon will rise and at what time each
day. Our modern view of the electron differs from this model.
Actually the electron occupies an `orbital' and instead of being
able to predict where the electron is relative to the nucleus,
our model of the electron requires us to think of the probability
of finding the electron at a certain position around the nucleus.
The electron occupies an orbital and the orbital has 3-dimension
shape. The electron has a high probability of being found within
the 3-dimensional space defined by the orbital. There are several
different types of orbitals which an electron can occupy, and
each different type has a different 3-dimensional structure.
Why do we use a 3-dimensional probability distribution
(orbital) to describe the electron rather than a 2-dimensional
orbit? The reason lies in our view of the nature of the electron.
In our previous discussion of the electron and its discovery by
J.J. Thomson we describe the electron in terms of its particle
properties. we thought of it in terms of its charge and its mass.
However, subsequent experiments by Thomson and others revealed a
dual nature of the electron. It could also exhibit wave
properties. Wave properties which suggested it behaved like
light.

So how do we view light and its wave properties? First we'll
discuss wave properties (Shockwave file)
then we'll look at light. Light that our eyes are able to dedect
is only a small part of the total range of electromagnetic
radiation. The electromagnetic spectrum (Shockwave file) (Physics
WEB Site) shows the range and where visible light is located.
Wave motion of light and wave motion in or fluids is general
described as traveling waves.
The light given off by elements when they are heated in a
flame, the light from the sun, are all examples of radiant
energy which is also called electromagnetic radiation.
Electromagnetic radiation is composed of electric and magnetic
components and exhibits wave properties (Wave Example file). In more general
terms a wave is a continuously repeating change or oscillation of
matter or a field in which the oscillation occurs. Light is
thought to consist of an electric and a magnetic component, each
at right angles to one another. Light exhibits wave character
because it is bent when it enters a glass prism. When white light
is focused on a prism it is separated into its component parts as
each part is bent to a different angle as it passes through the
prism.
So we need to have a clear understanding of waves. Waves are
not unfamiliar to any of us, particularly if you have spent any
time at the lake or swimming pool. Water exhibits characteristics
of waves. A calm surface in a pool, lake or pond can be set into
wave motion by a pebble or rock. Dropping the object into the
water produces ripples (waves) emminating from the point of entry
of the rock. We see these waves and we know they can transfer
energy. If you have ever been hit by a wave you know it can
transfer energy. But in our example of the lake, a leaf on the
water surface near the point of entry can be set into motion when
the waves make contact with it. So waves carry energy. We
characterize waves using four important properties; wavelength,
amplitude, frequency and velocity.
The animation (Wave Example file)
shows a simple two dimensional representation of a wave. Although
electromagnetic radiation is composed of magnetic and electric
components, we will simplify this and only consider the electric
component. According to our definition of a wave it is a
continuously repeating change or oscillation of matter or a
field. And we see how in this representation the wave is
oscillating. Lets look at the four properties of a wave.
First is its wavelength (Physics
WEB Site). The wavelength is the distance between
repeating points on the wave and the symbol, 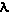 is used. For light in the visible region the
wavelength are very small and the unit used is the nanometer.
is used. For light in the visible region the
wavelength are very small and the unit used is the nanometer.
Amplitude is the distance between the highest (or lowest)
point on a wave and the center of the wave. In the two waves
shown, even though they have different wavelengths they have the
same amplitudes. If we consider light in the visible region the
amplitude controls the brightnest of light. The brighter the
light the larger the amplitude of the wave.
Frequency is the number of waves which pass a point in space
per unit time. The units of frequency are cycles per second (cps)
or hertz (Hz) [named after Heinrich Hertz a pioneer in the study
of electromagnetic radiation] and the symbol, 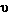 is used. Dividing the number of waves
passing the line by the time in seconds yields frequency. You
should notice that the shorter the wavelength for the
electromagnetic radiation the higher the frequency. The longer
the wavelength the lower the freqency.
is used. Dividing the number of waves
passing the line by the time in seconds yields frequency. You
should notice that the shorter the wavelength for the
electromagnetic radiation the higher the frequency. The longer
the wavelength the lower the freqency.
The velocity of a wave can be determined using the frequency,
the number of waves passing a point per unit time, and
wavelength, the distance between repeating points on the wave. If
we know how many wave pass a particular point per unit time and
we know the distance between the tops of the waves we can
calculate the velocity. Expressing this relationship
mathematically we have,

So if we know either the wavelength or the
frequancy for a sample of electromagnetic radiation we can
calculate the other. For example,
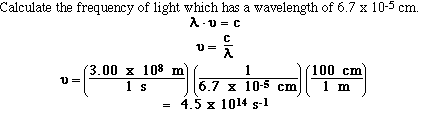

From a macroscopic viewpoint nature appears to be continuous.
If we go into the laboratory it is easy to measure 3.00 g of 24magnesium,
4.510 g of 24magnesium or any amount in between. On
the atomic scale however, this is not the case.
An analog to the example of magnesium is the appearance of a
sandy beach from a distance as a smooth, continuous surface. On
closer inspection however, the sand consists of individual grains
observable by the eye. If we look at our 3.00 g sample of 24magnesium
more closely we see the individual atoms of 24magnesium
each with a mass of 3.9822 x 10-22 g. We can not weigh
out anything but whole numbers of atoms of 24Mg.
Magnesium is not continous but comes in chunks called atoms.
In 1900 a total change in our view of matter occurred. One of
the ideas which lead to this change was quantization. While the
concept of a quantum was not new at this time it's application
into new areas would result in some significant changes. We
already have a feel for quantum, the atom is a quantum (bundle)
of matter. Also atoms have integer numbers of electrons. We can
not have atoms with 1/2 or 1/3 or 1/56 of an electron. Electrons
exist as discrete bundles.
Atoms are considered quanta of matter.

In the late nineteenth century Max Planck and Albert Einstein
realized that not only is matter quantized but energy and light
could also be interpreted as quantized. While the details of
Planck's pioneering work will not be discussed the results are
important. Planck had to resort to such a description to explain
experimental observations that he was collecting. Planck, as well
as others, had noted that when a metal, or solid or a dense gas
was heated they all behaved identically. They began by glowing
red and as heat was added glowed white. Planck wondered why this
occurred and set out to discover an answer. Planck studied the
light emitted by an object being heated. He noted that as an
object is heated it begins to glow giving off red light. If
heating is continued such the object gets hotter and the color
changes to orange and finally to white. Recall white is the color
associated with the presence of all colors of light. As an object
is heated it gives of red light first. Red light has the longest
wavelength and shortest frequency of visible light. Since this is
the color of light emitted when a small amount of energy is added
to the object Planck associated low energy with small frequency.
As the object is heated the energy of the light emitted increases
and other colors are produced until all colors of light are
produced and the object glows white.
Planck concluded that the energy gained or lost be an atom
must be some integer multiple of the minimum energy an atom can
give off. Planck argued that energy given off by an atom was
proportional to the frequency of light the atom emitted,
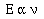
To convert the proportionality to an equality Planck added an
integer and a constant, now known as Planck's constant.
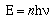
The integer n stands for the number of
photons of light. Usually this value is 1, or it can be
Avogadro's number (6.02 x 1023).
Light is composed of photons, which are small,
discrete bundles of energy. Planck imagined light as
composed of a stream of particles called photons.
Planck thought of each photon as a packet, or
quantum of energy. We feel this energy when stand
in the sun on a warm day.
The energy of a photon is proportional to its
frequency;

In this equation h is called Planck's constant and has a
value of 6.626 x 10-34 joule-seconds.
Example #1
A photon of orange light with a wavelength of 600 nm or
5.0 x 1014 sec-1 has an energy of;
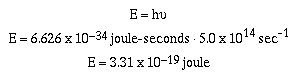
Red light also consists of a stream of photons, however, the
energy of this light is less than that of orange light because
the frequency is of red light is less than orange light. The
ideas were revolutionary, believe it or not. To suggest that
light was composed of small bundles of energy.
From this relationship it is apparent that the size of the
energy package, E, varies directly with the frequency of the
radiation. High frequency light in the visible spectrum, which is
violet, has the highest energy associated with it. Ultraviolet is
even higher frequency and higher in energy. Red light has a lower
frequency and also has lower energy. Recall that the frequency of
one of the doublets in the sodium spectrum was 5.085 x 1014
sec-1. This frequency corresponds to light of this
color (yellow) which comes in bundles of energy equal to 3.369 x
10-19 J. So light emitted from this line of the
doublet of sodium contains photons (quanta of light) of energy
equal to 3.369 x 10-19 J. If we have a higher
concentration of sodium in the solution the light is more
intense, or brighter, but the energy of the light does not
change.

Einstein had to apply the Planck's idea of quantization of
energy to understand the Photoelectric
Effect, behavior of ejected electrons from a metal surface
(orange lines) when light is shined on it. In the experiment
Einstein observed that as the frequency of light, shining on a
metal surface, is increased the energy of the electrons ejected
from the metal also increased. (Demonstrating how light has
particle properties) To explain the observations Einstein found
the idea of considering light as small packets, or quanta, or
massless particles helped him understand the effect. Einstein
suggested that light was quantized and each individual quantum of
light he called a photon.
However, there is a characteristic threshold which must be
achieved before any electrons can be ejected. When we consider
that light consists of photons, whose energy depends on its
frequency, in order to remove an electron from the metal a
certain minimum amount of energy must be acquired by the electron
before it is ejected. This experiment suggests that the
electrons that are around the atom, must absorb a certain amount
of energy before they can leave their stable arrangement.
In the early 20th century scientists were troubled as to how
atoms existed. According to classical arguments if the negatively
charged electron revolved around the positively charged nucleus
it would have to continuously loss energy, as electromagnetic
radiation (light), and spiral into the nucleus. But the atom did
not do this. In fact, as you recall, when atoms are placed in a
bunsen burner we observed electromagnetic radiation being given
off, not in a continuous way, but discretely, i.e. only certain
lines are observed.
Two workers in 1859, Robert Bunsen and Gustav Kirchhoff,
studied the light emitted by metals more closely using Bunsen's
newly designed gas burner. He and Kirchhoff studied the light
emitted by these metals by passing the light through a prism. The
light split into its component parts, but it did not appear
continuous, but as sharp lines. The sample tested by Bunsen and
Kirchhoff emitted light of specific wavelengths or frequencies.
Since the light seemed to come form the elements the spectra
where called emission spectra. The emission spectrum consists of
colored lines on a dark background. The spectrum of an element is
made up of spectral lines unique to that element. It was soon
discovered that passing an electric current between electrodes
sealed in a tube containing a vapor of an element in question
yielded the same spectra.
These observations by B and K shed new light on another
phenomenon called dark line spectra. When white light is passed
through samples of metal vapor, dark lines appear in a continuous
spectrum of the source. Careful measurement established that the
missing lines were identical to the emission lines of B and K.
The sodium vapor was absorbing the light. The conclusion: an
element can absorb or emit light of a particular frequency,
depending on the experiment.
The discrete nature of the emission spectrum of elements was
surprising. However, it was not clear at the time the
measurements were taken it was not taken too seriously. It was
surprising, but why elements behaved in this manner was not
immediately obvious. It wasn't until 1900 that these measurements
became a part of a revolution in how scientists looked at the
atom.
The light produced by the atoms occurs at specific
frequencies. Recalling Planck's relationship,

It is possible to calculate the energy of the photons emitted
by an atom. So if the frequency of the photon emitted by an atom
is large the energy lost by the atom is large, and visa-versa.
Niels Bohr, is credited with making the leap and determining
the regularity associated with the hydrogen atom emission
spectrum. Bohr combined classical physics with the quantum
concept to derive a relationship which describes the energy of
the hydrogen atom. Bohr recognized that Planck and Einstein's
ideas of photons and discrete energy state could be applied to
the discrete lines of the emission spectrum of hydrogen. Einstein
had shown that electrons could be ejected from a metal atom if
just enough energy could be supplied. Bohr assumed that the
emission spectrum of hydrogen was due to the behavior of the
electron in hydrogen. Bohr suggested the electron in a hydrogen
atom could only have certain energies, otherwise the atom could
emit light at all frequencies. In the flame the electron would
absorb some energy and emit it at the same frequency.
Bohr was suggesting the energy of the electron was quantized,
that is the electron could only exist in certain allowed energy
levels.
In order to reproduce the same equations determined empirical
by Rydberg and the others, Bohr formulated a model of the hydrogen atom where the
electron could only occupy certain energy states called
stationary states.
The important result for us which Bohr's model of atom
provides is that the electron could only exist in certain allowed
orbits. These orbits can also be called shells. When an electron
absorbed the correct amount of energy it could be excited from
one shell to another higher shell. The more energy the electron
absorbed the higher the shell and the further the electron is
from the nucleus. So if the electron absorbed the correct amount
of energy it could be excited from the first shell to the second
shell. That amount of energy was specific. If the amount of
energy was a littlemore or a little less the electron would not
be excited. Only the correct amount of energy could be absorbed.
Bohr's model said that the energy required to excite an electron
was quantized. Just as the distance each shell was from the
nucleus.
However, there was a problem. Bohr's model could not explain
the helium atom! Other chemists began looking at the problem. One
of them, Schrodinger, found that when the electron was treated as
a wave, not as a particle, something interesting was introduced.
Schrodinger's results indicated that not only could the electron
occupy a particlar level, but it could also occupy a particular
sublevel in each level, and within each sublevel it could be in a
particular orbital. This was getting very complicated. Yet the
experimental evidence sggested that this could be the only way to
think of the electron in an atom...as a wave.
The efforts by Schrodinger and others is as follows...the
electron can be in any level, for example the first or second or
third or even the fourth level. Each level contained at leastone
sublevel. In fact, the number of sublevels possible in a
particular level depended on the level the electron was in. If
the electron was in the first level, it could only be in one
sublevel. If it was in the second level, there were two possible
sublevels the electron could occupy. If the electron was in the
third level, there were three possible sublevels. The sublevel
are given letter names like, s, p, d,
or f. In the first level there is only one sublevel, the
s sublevel. In the second level there are two sublevels,
an s and a p. In the third level there are
three sublevels, s, p, and d.
Finally each sublevel has a different number of orbitals the
electron can be located in. Remember an orbital is a region of
space (3D) where the probability of finding the electron is high.
Any s sublevel contains a single orbital, a p
sublevel contains three orbitals, and a d sublevel
contains 5 orbitals.
So if an electron is in the first level it must be in the
single orbital of the s subshell. If it is in the second
level it could be in either an s or a p
subshell. If it is in the s subshell in the second level
it can only be in one orbital. If it is in the p
subshell it could be in any of three possible orbitals.
![]()