In Chapter 11 we established the theoretical organization to the periodic table, based on our knowledge of the electronic arrangement of multi–electron atoms. So what's next?

It turns out that as interesting as our quantum mechanical model of the atom is; there is more. If all we studied were the electronic arrangements of atoms, chemistry would not be as interesting as it is. Because the core of chemistry is interested in the thousands of combinations and permutations which can be made from the hundred–odd elements in the periodic table. We most commonly encounter the elements, not as pure substances, but as constituent parts of compounds. They can be simple like water (H₂O), carbon dioxide (CO₂) and sodium chloride (NaCl). Or complex as in proteins, nuclei acids or fatty acids. However, simple or complex all compounds are formed of aggregates of atoms combined in some characteristic ratio.

When Dalton first formulated his basic ideas on bonding 150 years ago, he was uncertain of the nature of the attractive forces which held atoms together. At first only naive pictures of hooked atoms interconnected with each other were used. Our present model really did not evolve until an understanding of the illucidation of the atomic structure of the atom. It is from this vantage point that we're able to gain the perceptions needed to view the combination of chemical elements.

Our present model of bonding is very sophisticated, but has its basis on the interaction of the valence electrons on atoms. Inner-core electrons feel large attractions to the nucleus, so it is only the valence electrons that become involved in bonding. The number of valence electrons associated with the atom of a representative element (any Group with an 'A' designation) is obtained from its Group number. For example, elements in Group IA have one electron in their outer-most orbital, and have one valence electron. Group VIIA elements, the halogens, have seven valence electrons.

A pictorial representation of the number of valence electrons on an atom can be shown with a Lewis structure. The Lewis structure representation is very, very important tool to enhance our view of simple chemical compounds.

Interestingly enough, our study of the reactivity of the elements will begin with that group of elements that are the least reactive–the inert gases. The secret to their stability can be found in their electron configuration. As they contain fully filled electronic shells/sublevels. Helium has a 1s² configuration, Ne is 1s²2s²2p⁶ each having completely filled shells. In argon it is true the 3d orbitals are unfilled, but those orbitals that are occupied are filled to saturation. The electrons are held tightly and as we have noted from ionization energies and electron affinities there is little desire to add to or remove electrons from their arrangements. Quite clearly these configurations exhibit unusual stability.

However, this stability of the elemental form does not occur in the two groups which flank the noble gases–the halogens and the alkali metals. We've already seen demonstrations showing the reactivity of members of both of these groups of elements. Moreover, although we have not studied these reactions, these two groups have a particular propensity to react with each other. And when doing so it is always to form a compound inwhich the atomic ratio is 1:1. Sodium chloride, NaCl, is of course the most familiar example.

All of the alkali metal halides share a number of common distinguishing properties. They are all crystalline solids with high melting points (600 – 1000 C). Suggesting they are held together by strong forces. When the solids are melted the liquid is found to conduct electricity. It is possible for electrical current to be carried by charged particles. And it was Faraday who carefully studied such behavior. Additionally he found that when a current was passed through a liquid, in the case of NaCl, sodium was attracted to the cathode (negatively charged electrode) and the chloride was attracted to the anode (positively charged electrode). All of this suggesting that the sodium in sodium chloride was not ordinary but existed as charged atoms, or ions, and they were called cations as they were attracted to the cathode. Similarily the behavior of the chloride suggested it was negatively charged and they were called anions.

These observations were supported by other experiments. In general the alkali metal halides dissolve readily in water. The solvent, H₂O, promoting the collapse of the crystalline solid and the separation of the charged ions. The resulting solution which contains Na⁺ and Cl^- ions readily conducts electricity. Such soluble salts, which conduct electricity, are called electrolytes. The formation of the ions in solution by electrolytes is characterized by the following equation;

NaCl_(s) ---H₂O --> Na⁺_(aq) + Cl^-_(aq)

For sodium chloride there are ions in the pure liquid and in solution, the ions must also be present in the solid. And we can rely on more than inference to support our predictions. Solid state characterization have revealed a characteristic arrangement of charged ions whose structures is;

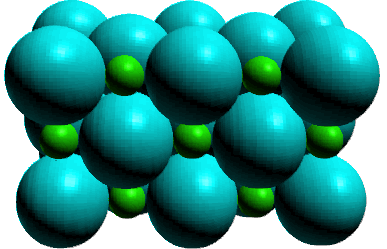
Because of the ion nature of these compounds they are called ionic compounds. The interaction between the cation and the anion that occurs in the solid state is called an electrostatic attraction between the positively charged cation and negatively charged anion. This electrostatic attraction is called an ionic bond. How do we visualize the formation of the charged ions? If we consider the reaction between a sodium atom and a chlorine atom, we can write

Na + Cl -----> Na⁺ + Cl^-

To understand the nature of the ions formed and the basis for the ionic bond we can write the respective electron configurations.

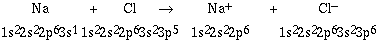
Another way to write the equation is to use electron-dot symbols or Lewis symbols. These symbols are a convenient way to indicate the number of valence electrons and help keep track of electrons during bond formation. In the equation we are considering sodium has 1 valence electron (1s²2s²2p⁶3s¹) because of the single electron in its outer most shell. We can write a Lewis structure for sodium as;

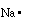
This indicates sodium has one electron in its outer most shell. Chlorine has seven valence electrons in its outer most shell (1s²2s²2p⁶3s²3p⁵). We can write a Lewis structure for chlorine as;

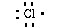
Sodium loses an electron and chlorine gains an electron. As a result of the transfer of the electron each now has a noble gas configuration and has little tendency to react further. The sodium is so intent on achieving a noble gas configuration that it will readily lose an electron. Chlorine is interested in gaining an electron to achieve the noble gas configuration. Recall that chlorine has a high tendency (electron affinity) to gain an electron and sodium has a low ionization potential.

The new Lewis symbols are;

Also notice the new electron configuration for the ions. Sodium is 1s²2s²2p⁶ and chlorine is 1s²2s²2p⁶3s²3p⁶. Each has eight electrons in its outer most shell. Each has an octet. The two elements have lost (sodium) or gained (chlorine) electrons to achieve an octet of electrons. We will observe the in simple terms much of the chemistry of the elements can be understood in terms of this relatively simple magic number of electrons. Of course hydrogen does not gain or lose electrons in the same manner. Since its nearest noble gas is helium, hydrogen will either lose (most often) one electron or gain one electron. This is called the duet rule.

Remember the octet rule is simply a summary statement of the observation that electrons are transferred such that elements achieve an octet of electrons. It is not a driving force in itself. It is simply a rule to help us make predictions and to summarize a large amount of data with a simple statement.

Another example can be given to examplify this behavior. We'll consider the reaction between a magnesium atom and an oxygen atom.

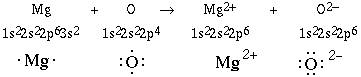
These two ions are both isoelectronic (same electronic configuration) with the neon atom. Again the ratio of ions in magnesium oxide will be 1:1 because of the identical magnitude of charge on both atoms. This is an example inwhich magnesium is oxidized (loss of electrons) and oxygen is being reduced (gain of electrons).

Here is one more example using lithium and fluorine.

Notice the electron lost by the metal is removed from the outer most orbital, the 3s orbital. For transition elements the loss of the electron is also from the outer most orbital, but care must be taken. Consider the element manganese, Mn, with the electron configuration of 1s²2s²2p⁶3s²3p⁶4s²3d⁵. In the transition metal elements it is unlikely, and the chemistry of these elements bare this out, that electron loss will occur to attain an inert gas configuration. However, the transition elements do lose electrons. When this occurs the first electron to be lost comes from the 4s orbital, as does the second electron, then any further electron loss comes from the d orbitals. So Mn²⁺ has the electron configuration of 1s²2s²2p⁶3s²3p⁶3d⁵, Mn³⁺ has the electron configuration of 1s²2s²2p⁶3s²3p⁶3d⁴.

Lattice Energy: Strengths of Ionic Bonds

Although there are several important factors which must be considered in determining the energy associated with forming ionic bonds, the lattice energy is were we will focus. The lattice energy is defined as the energy liberated in the following reaction;

Mⁿ⁺_(g) + X^m-_(g) ---> M_mX_n(s)

_{Lattice Energies of Alkali Metal Halides (kJ mol}-1₎

_{Lattice Energies of Salts of F}- _{(kJ mol}-1₎

The lattice energy is the energy liberated when oppositely charged ions in the gas phase come together to form a solid. So for sodium chloride the lattice energy is 787 kJ mol^–1. This is the energy liberated when Na⁺ and Cl^– ions in the gas phase come together to form the lattice of alternating Na⁺ and Cl^– ions in a NaCl crystal.

The charges and sizes of the ions are the critical factors which determine the magnitude of the lattice energy. The lattice energy is related to the potential energy of two interacting charges which is given in the mathematical equation;

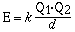
Q₁ and Q₂ are the magnitudes of the charge on the particles in coulombs and d is the distance between centers in meters. The constant k has a value of 8.99 x 10⁹J m C^–2. From this relationship the magnitude of the lattice energy is directly related to the charge on the ions and inversely related to the ionic radii of the ions. The combination of a small anion and a small cation liberates more energy compared to the combination of large ions. In general holding one of the ions constant the trend in lattice energy is reflected in the change in size of the counterion. The strength of the ionic bond also depends on the magnitude of the charge on the cation or anion. In the case of the fluoride compounds of sodium, magnesium and aluminum there is a dramatic difference in the lattice energy with cation charge.

It is the formation of the ionic bond which is the driving force for this reaction. In the solid sodium chloride considerable energy is liberated as a result of the arrangement of the sodium and chloride ions.

To generalize this electron lose and electron gain behavior we should note that Group IA metals, with their single valence electron will easily lose the electron to form a +1 cation. A behavior that continues down the Group. Group IIA metals will lose their two valence electrons to form M²⁺ cations. When this occurs the cations are isoelectronic with the preceeding noble gas. Group IIIA metals form M³⁺ species, although as we go down the Group we do see M⁺ species appearing. Removing 3 electrons requires considerably more energy, and as a result we see fewer ionic compounds in Group IIIA compared to Group IA and Group IIA.

Group IVA and VA exhibit little tendency to lose or gain electrons to form ionic bonds. Members of these two groups prefer to share electrons.

In Groups VIA and VIIA, elements with high electron affinities, we see gain of electrons to become isoelectronic with the next noble gas. Group VIA gaining two electrons and Group VIIA gaining one electron.

Ionic Radii

Before continuing we should consider the radii of the ions (common cations/common anions) formed when electrons are lost or gained by neutral atoms. The cation formed when one or more electrons are lost has a smaller ionic radius compared to the neutral atom. The loss of electrons increases the effective nuclear charge of the electrons remaining on the ion and they experience a greater attraction towards the nucleus. Adding of one or more electrons to a neutral atom, to form an anion, decreases the effective nuclear charge of the valence electrons and the ionic radius is greater compared to the neutral atomic radius. For isoelectronic ions the greater the positive charge the smaller the ionic radius. While for the isoelectronic ions the greater the negative charge the larger the atomic radius.

Same number of valence electrons in Be and B⁺, however the valence electrons in B⁺ 'see' a greater effective nuclear charge and are attracted closer to the nucleus––smaller radius than Be.

Same number of valence electrons in Ne and F^–, however the valence electrons in F^– 'see' a smaller effective nuclear charge and are not held as tightly by the nucleus––larger radius than Ne.

Some elements which form ionic compounds are too far removed from a noble gas to readily achieve the rare gas configuration. Members of the transition metals series would have to lose a large number of electrons to become isoelectronic with the nearest noble gas. Most transition metals form cations of 2+ and 3+. This suggests that stable ions can exist which do not duplicate the electronic arrangements of the noble gases. Some of the ions can be characterized by filled subshells, for example, Zn²⁺ [Ar]3d¹⁰, Ag⁺ [Kr]3d¹⁰ and Pb²⁺ [Xe]6s²5d¹⁰. It is therefore more difficult to predict most stable ions in the transition metals. Instead their chemistry is a collection of a large variety of ionic compounds.

Covalent Compounds

As important and varied as ionic compounds are, there are many compounds which do not demonstrate the high melting points, high water solubility and electrical conductivity of ionic compounds. This other group of compounds consists of examples that are gaseous, liquids and solids at room temperature, and generally they have low melting or boiling points. Frequently they are insoluble in water. They do not conduct electricity in the liquid state, or when soluble in water, do not conduct electricity in aqueous solution. Compounds that do not conduct electricity are called nonelectrolytes. There is no evidence to indicate that the elements in these compounds are ionic. Rather there is considerable experimental evidence to suggest that such compounds are made of discrete molecules, hence compounds in this group are called molecular compounds.

The forces that hold the atoms together in molecular compounds can not be understood on the basis of oppositely charged ions. So it was that Gilbert Lewis proposed that the strong attractive force between two atoms in a molecule reselted from a covalent bond, formed by sharing of a pair of electrons between the atoms in the bond.

In hydrogen, H₂, as the two hydrogen atoms approach one another their spherical 1s orbitals begin to overlap. Each electron occupying the space around the two nuclei. Each electron is attracted simultaneously by each nuclei. The attraction that bonds the electrons to both nuclei is the force holding the atoms together. Thus while ions do not exist in covalent compounds the bond can be regarded as arising from the attraction of oppositely charged particles–nuclei and electrons.

We can represent the formation of the covalent bond in hydrogen by writing the Lewis electron–dot formula for the atoms and the molecule.

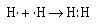
The two electrons between the two hydrogen nuclei represent a covalent bond. And the two electrons are referred to as an electron pair. Each hydrogen atom can be thought of as sharing the pair of electrons. When we think in these terms we note that each atom has a 1s² electron configuration, isoelectronic with the next noble gas–helium.

The formation of the covalent bond in gaseous HF can be described in similar terms;

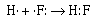
The fluorine atom and the hydrogen atom each require one electron to achieve a configuration isoelectronic with a noble gas. Helium for hydrogen and neon for fluorine. The two atoms share the electron pair to achieve their respective noble gas configurations. The other three pairs of electrons around the fluorine atom are called nonbonding or lone pair electrons.

Lewis Structures

• Rules