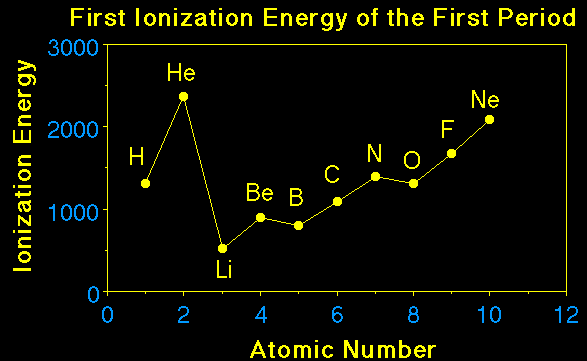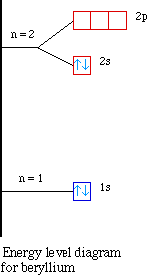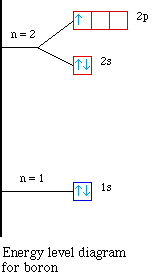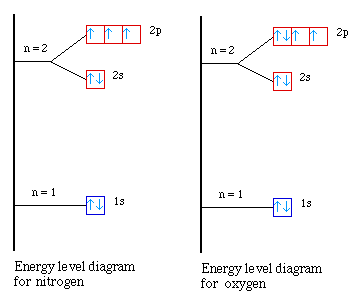
Element |
Nuclear
|
Electron
|
Inner Core
|
Valence
|
Effective Nuclear
|
Na |
11 |
1s22s22p63s1 |
10 |
1 |
+1 |
Mg |
12 |
1s22s22p63s2 |
10 |
2 |
+2 |
Al |
13 |
1s22s22p63s23p1 |
10 |
3 |
+3 |
Si |
14 |
1s22s22p63s23p2 |
10 |
4 |
+4 |
P |
15 |
1s22s22p63s23p3 |
10 |
5 |
+5 |
S |
16 |
1s22s22p63s23p4 |
10 |
6 |
+6 |
Cl |
17 |
1s22s22p63s23p5 |
10 |
7 |
+7 |
Ar |
18 |
1s22s22p63s23p6 |
10 |
8 |
+8 |
![]()
Element |
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
I7 |
Na |
490 |
4560 |
|||||
Mg |
735 |
1445 |
7730 |
||||
Al |
580 |
1815 |
2740 |
11,600 |
|||
Si |
780 |
1575 |
3220 |
4350 |
16,100 |
||
P |
1060 |
1890 |
2905 |
4950 |
6270 |
21,200 |
Element |
Electron
|
Electron
|
Inner Core/
|
Effective
|
Na |
1s22s22p63s1 |
3s |
1s22s22p63s1 |
+1 |
Na+ |
1s22s22p6 |
2p |
1s22s22p6 |
+9 |