It is OK to
use your textbook, but if you can answers the questions without it that is OK
too.
I recommend you print out this page and bring it to class. Click
here to show a set of five student responses, randomly selected from
all of the student responses thus far, in a new window.
, here are your responses
to the PLE and the Expert's response.
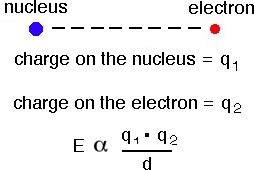
According to Coulombs Law the potential energy (E) between two
stationary charged particles is approximated by the equation shown above, where q1 and q2 are the charges on the particles (for example -1 charge for an
electron and a +1 charge for the nucleus), d is the separation between the charged particles in picometers
(1 pm = 10-12 m).
The first ionization energy is defined as, 'the amount of energy
required to remove an electron from a neutral atom.' The equation that was
written to describe this process for a general atom A in the gas phase is,
A(g) = A+(g) + 1e-
For the element hydrogen the equation describing the ionization energy would be,
H(g) = H+(g) + 1e-
The 1st ionization energy for hydrogen is 1312 kJ mol-1. This can be represented in the following figure.
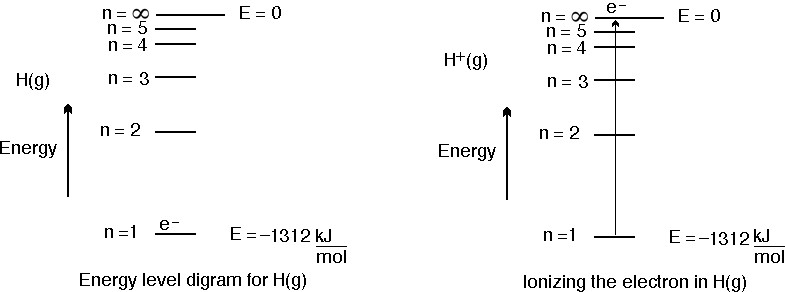
In the figure above the energy level diagram for a hydrogen atom is shown on the left. The one electron in hydrogen is shown in the n = 1 level. To remove the electron (shown on the right side of the figure, 1312 kJ/mol of energy is required to remove the electron from the hydrogen atom.
1. The 1st ionization energy for helium is 2372 kJ mol-1.
He(g) --> He+(g) + 1e-
Which of the following is the best explanation for why the 1st ionization energy for helium is nearly twice the 1st
ionization energy for hydrogen.
If the two electrons in helium are at approximately the same distance from the nucleus as the electron in hydrogen, and there are twice as many protons in the nucleus of a helium atom as there are in the nucleus of a hydrogen atom one would expect the 1st IE is approximately twice that of hydrogen's 1st IE.)
2. According to Coulombs Law what happens to the magnitude of the ionization energy as the nuclear charge (number of protons) increases?
(Since there is an electrostatic attraction
between protons and electrons due to their opposite charges (see the mathematical
equation at the beginning of the BCE) one would expect the energy required to
remove an electron to increase as the nuclear charge increases.)
3. According to Coulombs Law what happens to the magnitude of the ionization energy as the electrons get further from the nucleus?
(as the electron gets further from the
nucleus is experiences less attraction to the nucleus (see the mathematical
equation at the beginning of the PLE). The electron is higher in energy the
further from the nucleus, so it takes less energy to remove the electron the
further it is from the nucleus.)
4. Consider the element lithium, if we assume that the three electrons in lithium are the same distance from the nucleus as the electrons in hydrogen and helium estimate the 1st ionization energy for lithium?
(Lithium's 1st IE will be greater than
helium's and hydrogen's 1st IE. If lithium's 1st IE only depended on the nuclear
charge, assuming the electrons are the same distance from the nucleus as the electrons in hydrogen and helium, is would be about three times the 1st IE for hydrogen and 1.5 times
greater than helium's 1st IE, so near 3400 kJ mol-1.)
5. The first ionization energy for lithium is actually known to be
520 kJ mol-1. Comparing this 1st IE to the 1st IE's for hydrogen
and helium, how would you explain lithium's 1st IE based upon the ideas
presented in Q2 and Q3 above.
(The actual 1st IE for lithium is 520
kJ mol-1. It is actually lower than hydrogen's and helium's 1st
IE. The only way this could be is if the electron removed is further from
the nucleus, in a different shell compared to the electrons in hydrogen and
helium.)
6. The first ionization energy for beryllium is known to
be 899 kJ mol-1. The electron that is removed from beryllium must be;
(Since the 1st IE for beryllium is greater
it must be in the same shell as lithium's. A higher 1st IE is due to a greater
attraction to the nucleus. So the higher 1st IE for beryllium is due to the
greater nuclear charge in the beryllium nucleus. Compared to the 1st IE for
hydrogen and helium, beryllium's 1st IE is still smaller. So the first two electrons
in beryllium are in a level closer to the nucleus than the second two electrons.)
7. The 1st ionization energies as we continue
across the periodic table from boron (800 kJ mol-1) to neon (2081
kJ mol-1) continue to (in general) increase. What factor(s) best explain this general increase as we proceed from boron to neon?
(The increasing nuclear charge factor is
the only factor that explains an increase in the 1st ionization energy. So going
from lithium to neon there is an (in general) increase in the 1st IE. So all
of the electrons added from lithium to neon are going into the same shell.)
8. The atom following neon in the periodic table is sodium.
Its 1st ionization energy is 495 kJ mol-1. How would you explain
this ionization energy?
(Since the 1st IE for sodium is now considerably smaller
than the 1st IE for neon, the 11th electron must be added to a new shell.
In this case it is the third shell. The pattern we are seeing is that there
are two electrons in the first shell, and eight electrons in the second shell.)
9. Would you predict there to be a steady increase, decrease
or no change in the 1st IE's for elements as we move from Na to Ar?
(Based on the behavior of the 1st IE's
of lithium to neon the 1st IE's from sodium to argon should also increase. All of
these electrons will be in the same level.)
10. Is there anything about the questions that you feel you do not understand?
List your concerns/questions.
11. If there is one question you would like to have answered in lecture, what
would that question be?


