2nd and 3rd Laws of Thermodynamics Lecture Notes

In this Chapter we return to a discussion of thermodynamics, the study of heat and energy flow.

The thermodynamics that we have discussed in CHEM 1314 included the concepts of endothermicity and exothermicity. As a start let's review the concept of endothermic and exothermic as applied to chemical reactions. To determine whether a particular reaction is endothermic or exothermic we can calculate the H^o_rxn for the reaction of interest. (To review calculating H^o_rxn check out this lecture from CHEM 1314.) If the sign of H^o_rxn is negative the reaction is exothermic, releasing heat to the surroundings. If the sign of H^o_rxn is positive the reaction is endothermic, absorbing heat from the surroundings. Experimentally, if we measure the temperature of the reaction as it occurs and temperature of the reaction increases, the reaction is releasing heat (exothermic), if the temperature of the reaction decreases, the reaction is absorbing heat (endothermic).

This semester with the exception of one chapter we will be applying the ideas of thermodynamics. We discussed the first law of thermodynamics in CHEM 1314. We learned about calorimetry and the idea that energy could not be created or destroyed. We used the first law to determine the enthalpy change in a chemical reaction. That is whether it was exothermic (heat flow from system to the surroundings) or endothermic (heat flow from the surroundings to the system). We used the specific heat of water, and the heat capacity of calorimeters to determine the heat flow at constant pressure (enthalpy) and the heat flow at constant volume (internal energy).

            We used enthalpies of formation and the mathematical equation

to calculate the enthalpy change for a chemical reaction. There were several problems on the review problem set that require you to apply your understanding of the first law of thermodynamics.

        This semester we need to spend some time discussing the second and third law of thermodynamics. We will introduce the concept of thermodynamic favorability (free energy) and entropy change (dispersal of energy and position).

       In CHEM 1314 when we mixed hot water and cold water, we knew intuitively that the temperature of the hot water would decrease and the temperature of the cold water would increase. We know, from experience, that heat flows from a hot object to a cold object. Another example would be ice in a glass of soda. If placed on a table in a room at room temperature, after a period of time we would expect the ice to melt. Such a change is thermodynamically favored. We would not expect the glass of soda and ice to become frozen or a slush while on the table. Thermodynamically favored, for a chemist, means that a particular change, physical or chemical will occur without outside intervention. Historically, the word spontaneous has been used to describe a physical or chemical change that is thermodynamically favored. Today, the word spontaneous has been replaced with thermodynamically favored. In the English language, spontaneous, means a behavior that occurs without planning. Someone who is spontaneous is also impulsive, uninhibited. For a chemist we want to know whether a chemical change is thermodynamically favored or not.

In this Chapter we are more interested in reactions that occur on their own, and reactions or changes that can not occur on their own. For example consider two reactions we have seen before;

2Na(s) + Cl₂(g) ---> 2NaCl(s) H^o_rxn = -822 kJ mol^-1

CH₄(g) + 3O₂(g) ----> CO₂(g) + 2H₂O(l) H^o_rxn = -890 kJ mol^-1

Both of these reactions are very exothermic. Both of these reactions are thermodynamically favored. The word thermodynamically favored means something very specific when we discuss thermodynamics. thermodynamically favored means, a tendency to proceed in one particular direction unassisted. A reaction considered thermodynamically favored is one which proceeds from reactants towards products without any assistance. This is the case for these two reactions. A reaction that is not thermodynamically favored would be the following;

CO₂(g) + 2H₂O(l) ----> CH₄(g) + 3O₂(g) H^o_rxn = +890 kJ mol^-1

We would never expect to see carbon dioxide mixed with water producing methane gas. One difference, thermodynamically, between these two reaction is that one is exothermic and the other is endothermic. Could we use the enthalpy change, H^o_rxn, to predict whether a particular reaction is thermodynamically favored or not (assuming we could not test the reaction ourselves). Reactions that are exothermic are reactions where the reactants are at higher energy compared to the products. Going from reactants to products releases the difference in energy to the surrounding, so why not?

It would be like allowing an object at high potential energy to fall/move downhill (in energy), by dropping the object. That is a thermodynamically favored process and the reverse of that process is not thermodynamically favored.

At first glance it actually looks reasonable. However, there are reactions that are endothermic that can occur unassisted, and therefore are thermodynamically favored. One example is the reaction;

So we can not use our knowledge of H^o_rxn to determine whether it is thermodynamically favored or not.

Some other examples are useful. Consider the following physical changes;

H₂O(l) ----> H₂O(s)

H₂O(s) ----> H₂O(l)

The first is exothermic and the second is endothermic. Below 0 degrees Celsius liquid water is thermodynamically favored to convert to the solid phase (freeze), yet above 0 degrees Celsius liquid water will not freeze. The conversion of water in the liquid phase to water in the solid phase is thermodynamically favored when the temperature of the system is below 0 degrees Celsius, but not thermodynamically favored above 0 degrees Celsius. Similarly, above 0 degrees Celsius water in the solid phase is thermodynamically favored to melt, but not when water is in the solid phase below 0 degrees Celsius. Both changes are thermodynamically favored at slightly different temperatures, under different conditions.

The process of dissolution of solids in water is generally endothermic, and we know lots of ionic solids that dissolve in water.

NaCl(s) --H₂O(l)--> Na⁺(aq) + Cl^-(aq)

So whether a reaction is endothermic or not may not be the best predictor of whether a reaction is thermodynamically favored or not.

Is there anything interesting about these systems that were endothermic, yet thermodynamically favored? Lets look at those reactions more carefully;

Ba(OH)₂.8H₂O_(s) + 2NH₄SCN_(s) ---> Ba(SCN)_2(aq) + 2NH_3(aq) + 10H₂O_(l)

H₂O(s) ----> H₂O(l)

NaCl(s) --H₂O(l)--> Na⁺(aq) + Cl^-(aq)

In the first case there are three moles of reactants going to 13 moles of products, and the reactants are both solids and the products are liquid, gas, or dissolved. In the second change water in the solid state changes to water in the liquid state, and finally the sodium chloride, in the solid state, dissolves forming ions in solution.

In each case the products are in physical states that is more dispersed compared to the reactants.

The phase of a substance is very important in making a qualitative prediction of the magnitude of the entropy of a pure substance. Below we will consider the three phase of matter; solid, liquid and gas in terms of the extent particles in these phases are dispered in terms of position and in terms of energy.

For a particulate level view of a solid we will look at a model developed by concord.org. Atoms in the solid state are in fixed positions. In the solid phase atoms, molecules, or particles can vibrate, but they can not rotate or translate. In the solid phase particules are not very dispersed in terms of their position. In terms of energy, or solids atomic energies are limited in range, only in vibrational modes. The limited amount of dispersion in position and energy results in the entropy of solids being very small.

It is this ability to be dispersed in terms of position and energy that is the key to our search to understand thermodynamic favorability.

The concept of dispersion is not that strange to us. What happens when a deck of cards is shuffled and five cards are dealt, what do you think is the chance that I might deal a straight flush? Not very good? Beginning with a deck of cards in rank order from ace to king of each suit, and then shuffling them. How long would I need to shuffle them back into order again?

If we shuffle the deck the cards those cards become more dispersed relative to their rank order from ace to king and their respective suits. In fact the more we shuffle the more dispersed the cards becomes. In fact there are 8.066 x 10⁶⁷ possible different ways to arrange the 52 cards in a deck of cards. When we shuffle, the probability that any particular order occurs is then 1 chance in 8.066 x 10⁶⁷. So there are lots of different possible arrangements of the cards. We can think of some ordered arrangements, but the number of disordered arrangements far out number the number of ordered arrangements. And in a deck of cards we are only concerned with 52 cards!

What about molecules and atoms? Here we are talking about really big numbers!! 6.023 x 10²³ in a mole of any substance.

Suppose we have a container separated into two compartments, one side with 20 particles on one side and none on the other side. If I open the door between the two compartments what would you expect the distribution of particles to be after a period of time?

Answer

Scientists use the concept of entropy to describe the number of different possible arrangements for a system. That is, entropy measures the extent to which a system is dispersed in position and energy. High entropy values indicate a high degree of dispersal.

In a chemical reaction if the products side of the equation the particles are more dispersed compared to the reactants the reaction is described as increasing in entropy, increasing in disorder. Greater dispersion of position and energy is the favored direction. The system with the 20 particles expanding into an evacuated container is an excellent example. There is no change in temperature in this system, before and after the removal of the barrier. The drive of the change is to disperse the particles to as great an extent as is possible. There is a greater volume for the particles so there are a greater number of arrangements of the positions of the particles.

It is in fact this natural tendency, towards greater dispersion that defines thermodynamic favorability in events, chemical or otherwise. We stated earlier the first law of thermodynamics, the second law is related to entropy.

the second law of thermodynamics states that thermodynamically favored natural processes are accompanied by an increase in the entropy of the universe.

When considering qualitative prediction in terms of entropy the most important factor is the phase of the substance(s) involved. The next most important factor is the number of particles involved. for example, in a chemical reaction where the phase of the reactants and products are the same we must count the number of reactant and product particles. If there are more particles in the products compared to the reactants, based on the coefficients, the change in entropy will be positive. The third factor to consider, when the phases and numbers of reactants and products are all the same, is the complexity of the reactants or products. Complexity can be determined by the number of different atoms in reactant or product molecules. We will consider a number of examples below to practice.

We can express this mathematically using the symbol for entropy, S, in the following terms,

S_universe = S_system + S_surrounding > 0

This relationship says that if we add the change in entropy for a system, like a chemical reaction, to the change in entropy of the surrounding, and that value is greater than zero the process is favored.

Thermodynamically favored processes have a S_universe that is greater than zero. So a chemical reaction (the system) may have a negative S, but as long as the S of the surroundings is positive and greater in magnitude compared to the S of the reaction the reaction will still be thermodynamically favored.

Since entropy is a measure of disperal we would expect something that is not very dispersed to have a very low entropy. This is the case. In fact this is the basis of the third law of thermodynamics,

the third law of thermodynamics says that the entropy of any pure substance at absolute zero is zero.

When we add heat to a pure substance the particles of that substance begin to vibrate and the solid begins to expand and the substance absorbs energy. When this occurs there is an increase in the how energy and position are dispersed among the collection of atoms of the substance and the entropy increases. Since the entropy of a pure substances depends on its temperature the units on entropy are joules Kelvins^-1.

We are most interested in the entropy of substances at 25 degrees Celsius and 1 atmosphere (standard state conditions).

Some entropy values for pure substances are shown below;

You should have some intuition about entropy values in terms of physical states, temperature, solution process and molecular complexity.

physical states - looking at the table above in general the entropy values for gases are larger than entropy values for liquids and for solids. Particles in the gas phase are more dispersed in energy and in position compared to a particles in the liquid phases and both liquid phase and gas phase are more dispersed than a solid. So we would expect that chemical reactions producing more gases compared to the reactants will have a positive S.

temperature - As discussed earlier about the third law of thermodynamics, the higher the temperature the greater the energy for the substance/system, and the more dispersed that energy can become.

solution process - dissolving solids in water/solvent generally leads to greater dispersal. So comparing NaCl(s) to NaCl(aq) in the aqueous solution the ions are more dispersed compared to the ions in the solid. However, there are some exceptions to this rule, some ions have a very large charge and when added to water, order the water molecules resulting in a more ordered state, or reducing the extent that water molecules are dispersed in the solution. Al³⁺ is an example of an ion that when dissolved in water produces a more ordered system. When gases dissolve in water the S is always negative. For example, O₂(g) has a higher entropy than O₂(aq).

molecular complexity - this is a more complicated issue. From the table above we can see some trends, for example, HF, HCl, HBr and HI. The entropy value increases going down the group. The more electrons in the molecule of similar structure the greater the entropy. We can also see a similar trend for CH₄(g), C₂H₆(g), and C₃H₈(g). In this case the molecule is getting more complex as CH₂ groups are added.

In a chemical reaction we are interested in the S of the reaction. An ability to judge in qualitative terms the sign of S is very important.

In a reaction if the products are more dispersed (in energy and position) compared to the reactants the sign of S is positive (+).

If the products are less dispersed (in energy and position) compared to the reactants the sign of S is negative (-).

There are several factors that must be considered when determining S for a chemical reaction.

1. Phase changes-this is the most important factor when determining the S for a reaction. If the product phase(s) are phase(s) where particles are more dispersed compared to the reactants S will be positive.

Example: What is the sign of S for the reaction;

2HgO(s) ----> 2Hg(l) + O₂(g)

S is positive (+) since a solid (reactants) is forming a liquid and a gas (products).

2. n (change in moles)-this is the next most important factor when determining S for a reaction. So if the chemical change can not be determined in terms of phases, doispersal is increased when there are more possibilities of where an element can be. So in a reaction the more moles of substance there are the greater the entropy (disorder).

Example: What is the sign of S for the reaction;

2H₂(g) + O₂(g) ----> 2H₂O(g)

In this reaction the products and the reactants have the same phase, so we can not use phase change to determine the S. There are two moles of products and three moles of reactants. Since there are fewer moles of products the reaction S is negative.

3. Molecular complexity-the last factor to consider, assuming there is no change in phase, and number of moles of product and reactants are equal, is the molecular complexity. The more atoms, the more variety of elements, and/or the more number of electrons all favor greater disorder.

Example: What is the sign of S for the reaction;

H₂(g) + Cl₂(g) ----> 2HCl(g)

In this reaction the the product and reactants have the same phase and there are equal moles of reactants and products. Molecular complexity must be the criteria used to determine the S. In this case HCl has great molecular complexity compared to H₂ or Cl₂ because the HCl has different elements. The difference in entropy between the reactants and products is small, but S is still very slightly positive.

So try your intuition on the following examples.

Predict whether S is positive, negative, or close to zero for the following changes.

a) 2H₂(g) + O₂(g) ----> 2H₂O(g) Answer

b) 2KClO₃(s) ----> 2KCl(s) + 3O₂(g) Answer

c) 2NO₂(g) ----> N₂O₄(g) Answer

d) CH₄(g) + 2O₂(g) ----> CO₂(g) + 2H₂O(l) Answer

When you have answered the above four sample you can try a few additional problems.

we also have to be able to calculate the value for S^o for a reaction. The equation we use to calculate S^o for a reaction uses the fact that entropy is a state function. Since entropy is a state function we can use Hess' Law to determine the S^o for a reaction. So the mathematical equation we use to calculate S^o for a reaction is;

Lets consider some sample problems.

Using the table of entropy values above, calculate S^o for a each of the following reactions,

a) 2H₂(g) + O₂(g) ----> 2H₂O(g) Answer

b) 2C₂H₆(g) + 7O₂(g) ----> 6H₂O(l) + 4CO₂(g) Answer

So we can calculate S^o for a reaction, but how does that help us determine whether a reaction is thermodynamically favored.?

The issue of thermodynamic favorability according to the 2nd law is related to the S_universe for a chemical or physical change. So the question is how do we calculate the S_universe? According to the 2nd law,

S_universe = S_system + S_surrounding > 0

We know how to calculate the S_system , we did that in the example above where we calculated the S^o for the reaction, 2H₂(g) + O₂(g) ----> 2H₂O(g). But how do we calculate the S_surrounding? That is a little more difficult.

Let's begin by thinking about S_surrounding from a qualitative stand point. The way we'll approach the entropy of the surrounding is to consider what happens when an exothermic reaction occurs in a container. An exothermic reaction is one in which the heat produced in the reaction is liberated/transferred to the surroundings. So the surrounding get hotter. We also know from our earlier discussion of entropy that as the temperature increases so does the entropy. So we can say mathematically that,

S_surrounding -q_surrounding

Additionally when heat is transferred to the surrounding and the surroundings are at a low temperature the effect on the change in entropy is much greater than when that same amount of heat is transferred to the surroundings when the surroundings are at a higher temperature. We can express this mathematically as,

S_surrounding

So combinning these two ideas we have,

If we are studying the reaction at constant pressure than q_surrounding = H_system.

So if we return to the original 2nd law equation,

S_universe = S_system > 0

this relationship can be re-arranged in the following way,

Now we will define a new function, called free energy (G) to represent -TS_universe and the relationship becomes,

G_system = H_system - TS_system > 0

The way we use this relationship to determine if a reaction is thermodynamically favored is to calculate H and S for the reaction of interest, then use the equation above to calculate G for the reaction. If G is less than zero the reaction is thermodynamically favored, if G is greater than zero the reaction is not thermodynamically favored.

We know how to calculate H and S for a reaction, so calculating G is not too difficult. Lets look at an example, by continuing with the reaction producing water for which we've already calculated S,

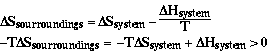
Sample Problem

Is the reaction below thermodynamically favored at 298 K?

a) 2H₂(g) + O₂(g) ----> 2H₂O(g) Answer

We can also calculate G for a reaction using an approach not to unlike the H and S, discussed earlier. The form of a second mathematical equation we can use to calculate G is,

Let's try a sample problem using this equation to calculate G.

Sample Problem

Calculate G for the reaction,

3NO(g) ---> N₂O(g) + NO₂(g)

Answer

One additional issue to consider for this particular reaction is the temperature dependence of G. The formation of water is exothermic (H is -) and becomes more ordered (S is -). Under these conditions the reaction is thermodynamically favored at low temperature and not thermodynamically favored at high temperature. But at what temperature does the reaction become not thermodynamically favored?

Sample Problem:

Calculate the temperature the reaction,

2H₂(g) + O₂(g) ----> 2H₂O(g)

becomes not thermodynamically favored. Answer